如下图MTF值跟离焦量有关系
空间频率为25pl/mm和10pl/mm的MTF曲线图
该曲线可拟合成一条抛物线，纽荷尔显微镜制冷相机油墨观察，其最大值对应的位置为最佳成像面位置，设该抛物线：
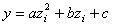
在多个像面测得MTF值的残余误差平方和为：
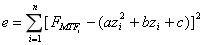
a,b,c为拟合系数;n为采样平面数;zi为离焦位置坐标.根据最小二乘原理,容易解得拟合系数a,b,c,并进一步算得焦平面位置：
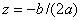
另一种方法是，在固定步长的条件下，纽荷尔显微镜制冷相机油墨观察，逐一查找不同位置的MTF值，同时记录下每个MTF值及其对应的位置，最终回到MTF值最大的地方。虽然这种方法相对耗时，但我们可以对其进行优化，这就是所谓的变步长搜索方法。首先，我们使用较大的步长来快速定位到MTF的最大值，然后在最大值附近使用较小的步长进行精细搜索。重复这个过程，直到达到预设的精度标准。虽然这种单向搜索的方法需要一定的时间，但它能够确保结果的准确性。此外，还有一种名为爬山搜索算法的方法可供选择。
显而易见，当对焦评价曲线受到外部因素的干扰，产生多个峰值时，传统的爬山法可能会错误地锁定在局部极值上，从而导致对焦失败。为了解决这一问题，康宗明等人提出了一种改进的爬山法。这种方法引入了“方向帧”的概念，并在对焦过程中结合了多种判据。这样的改进不仅提高了对焦的精度，还能有效避免单一判据在某些情况下可能失效的风险。
在Fibonacci 搜索的步骤中首先确定搜索区间L1 和最小分离度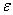
及试验点数n 计算步长：
F(n)代表Fibonacci函数。接着，从两侧端点开始，按照L2长度确定第一个试验点a1和第二个试验点b1。依据实验点处的评价值，我们决定删除左侧或右侧区间。随后，在剩余的区间上对称地选择下一次的试验点，并重复这一步骤进行n次试验。最后一个试验点与已有的试验点之间的距离，理论上定义了最终的不确定区间。
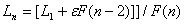
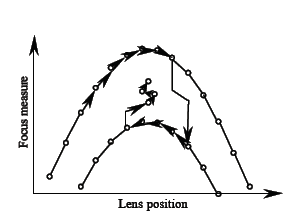
Fibonacci搜索在存储取样点方面占用资源较少，其不确定区间的预测相对简便，因此在给定试验次数的情况下，被视为最佳搜索策略。然而，当焦评价函数曲线并非理想的光滑曲线，而是出现大量的局部极大值时，Fibonacci搜索可能会陷入这些局部极大值的邻近区域，从而影响其搜索效果。
